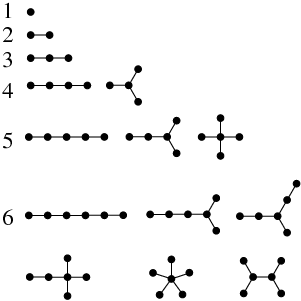
It all started when I found this picture, during one of my endless nights of wandering the web:

I though "Oah, that's very cool, I wonder how the list goes on...", and I continued the list by hand. It was a lot of fun trying to find all the possibilities, and at the same time removing the ones that were the identical, just not drawn the same. For 7, there was 11 of them. At 8, 23. For 9, it got to 47. Quite a nice way to pass the time during lectures, drawing dots! Repetitive work, despite allowing for meditation, is annoying. Repetitive work is perfect work for machines. I happen to know a bit about making machines compute stuff for me. Quite naturally, I wondered...
Can I make my computer draw all these dots for me?
A night of coding later, the magic occurred...
Graphs are awesome. Quite simply, they are defined as a set of vertices, or nodes, and a set of pairs of these vertices, called edges or arcs.
Graphs can be directed (if the edges have a direction) or undirected. Graphs can be simple, when only one edge can link two given nodes or pseudographs (with parallel edges). Graphs can be labeled (nodes have names) or unlabeled, graphs can be weighted (edges have numbers). Graphs are planar when edges don't intersect on a sheet of paper, graphs are regular if every node has the same number of neighbors, and complete, if all nodes are neighbors. Graphs are everywhere. The metro plan is a graph. The roads in Google Maps are a graph. The web is a graph. Your friends on Facebook are a graph. Wikipedia is a graph. The bots in your favorite shooter use graphs to move around, heck, even your coffee machine probably uses graphs to remember its state and avoid pouring cappuccino before putting a cup.
Graphs are everywhere. But in the end they're really just dots and lines.
Some graphs are particulars. They are simple, connected, and acyclic. Simple, we've covered already. Connected means that there is a path from each node to every other node. No separate sub-graphs playing solo. And acyclic, well, it means that no node is connected to itself. It is quite equivalent to saying that between two nodes there is one and only one path. It is also equivalent to saying that if you add an edge, there will be a loop. Or that if you remove one edge, you cut the graph in two separate bits.
These guys are called trees. Why? Weeell, if you check a tree, there is a high chance that all bits of the tree will be connected to each other (or then it is another tree), and for most normally constituted trees, there shouldn't be loops. If you cut a branch, well, you get a tree plus a branch. And if you glue a branch to another, it makes a loop. That sounds pretty reasonable.
Trees, as a sub-kind of graphs, are also very useful. Family trees, football championship trees, phylogenetic trees, decision trees, the diagram of your boss, and his boss, and his boss, until the boss of everyone is (often) a tree, the table of contents of a book is a tree, like the structure of a web page. Your web browser uses a tree to represent the pages. Your hard drive is a tree, with folders in folders in folders. You get the picture.
Now trees also come in several shapes, and have a lot of properties. For instance, a rooted tree is a tree with a root, that is, a special node that we chose to be "the root". Once we chose a root, we can describe the relation between all other nodes as "parent" and "child". The neighbors of the root are its children. The neighbors of these nodes (excepts the root) are their children. And the neighbors of these new (except the one we've already mentioned) are their own children, and so on. And of course, a node is a parent to its child.
A rooted tree is easy to represent: top down (or bottom up, for the tree analogy, but the other one is really more common. I think.) Put the root at the top, its children at second level, their children at third, etc. See how concepts emerge naturally: the depth of a node (how many hops to the root), the height of the tree (the depth of the deepest node). A node without children is usually called a leaf. A node can have only one parent, or none if it is the root. A n-ary tree (especially 2-ary or "binary") is a tree in which each node has exactly n children. A 1-ary tree is pretty boring: it's just a chain. They call it degenerate... A perfect tree has all its leaves at the same depth. There are plenty of other names like this.
A non rooted tree can be called a free tree. Depending on the context, "tree" might refer to either one. Since the ones that interest me (the ones in the picture up there) are unrooted, I'll usually say "tree" for "free tree", and add the "rooted" precision when necessary. But now that we covered the bases, let's get to serious business...
Representing data in a computer is both a fascinating and a very complex subject. How do I tell my computer about, say, the last tree of the first picture? The picture itself won't be very helpful. A bunch of black and white pixels don't say much about what they represent. Coordinates would be a bit closer then? The positions of the nodes, and the positions of the edges. But if I move one node a bit to the left, it's still the same tree, right? It might not look exactly the same, but on the mathematical point of view,
One of the first ideas we might have, is to use graphs. After all, trees are graphs, and inherit all the properties of graphs. Maybe we can find something there.
So, graphs! A bunch of nodes, and the edges that link them. Since our nodes won't carry any data (they're not used as a data structure, but as a mathematical construct), let's just number them from 1 to N (instead of allocating memory for each, and using pointers to reference them). Edges, a list of pair of numbers. Simple so far. For instance, for our little tree (let's call it Bob), we could have:
(1,2)(6,2)(2,3)(3,4)(5,3)
Stooop! We already have a problem. Can you see a problem? I added labels to Bob, because, well, the computer needs something to calls the nodes. We could allocate random memory for them and use only references, but it would become quite hard to say anything about anything. So I had to choose an arbitrary labeling of Bob. I could have chosen many others. For N nodes, there are N! ways to number them (factorial of N is N*(N-1)*(N-2)*...2*1. It's a number that gets really big really fast...). 720 possibilities for Bob! Actually it's less, because Bob is somewhat symmetric, and some numberings are equivalent, but still!
Bob is also (1,4)(6,4)(4,5)(5,2)(5,3)
If Bob has 720 names (or even less), how do I know that all of these names are its names? How can I find out if two different lists of edges are in fact the same tree (the cool kids say that these graphs are "isomorphic")? Bad luck. It is in fact a hard problem to solve, called (you'll never guess) the "graph isomorphism problem". It is possible, and solutions exists, but they take a lot of time, for a big number of nodes. And frankly, it seemed hard to code. So I didn't code it. Instead, I forgot about graphs. Because you see, trees are very specific graphs. Very simple graphs. They are a very small tribe in the world of graphs. Maybe there is an easier way to handle them.
Very close friends of the trees are the rooted trees. Some might say that free trees are cooler because they don't need a support, they can float in the airs, etc, but they're not so different. Each free tree of size N has indeed N rooted tree cousins, which if they ignored the fact that they had a root, would be very much all alike. Again, for symmetry reasons, some have less than N. For instance, Bob has only two rooted tree cousins:
If you replaced the double dots by normal dots, you would get two Bobs, right? So maybe if we can deal with rooted trees, we'd be really just a step away from the free trees. So be it. Rooted trees it is.
A very cool thing about rooted trees is that they are easy to represent in a computer. Because you see, you can define them recursively. For now, we've defined trees as graphs and rooted trees as trees with roots. That is: nodes + edges + simpleness + connectedness + acyclicness + one root. If you look at Bob's cousins up there, you might have the feeling that this definition is overkill. Take a look at this one (call her Alice):
Once you've noticed it, it gets very cool: recursivity. When we say that a node has children nodes, (which in turn have children too), we could really say that a node has children trees... And redefine a (rooted) tree as follows. "A tree is a set (possibly empty) of trees." We can describe the previous tree as "Alice is a tree with an only child: Orange". Orange, in turn, is a tree with two children: Pink, and an empty tree. Pink is a tree with two children, both empty.
In programming terms: a tree is a list of references to other trees. That's all we need to know (well, we still need to add that a tree cannot have an ancestor as child, of course. Otherwise that would actually make it a directed graph, since there would be loops, but it's really not a problem. Just don't try.) The implementation will be different in each programming language, but the idea is the same.
[Before we start, a little note: I programmed everything in Lua, a programming language that I particularly affectionate. But of course, any programming language would do the trick. Don't be surprised if the pseudo-code looks a lot like Lua at times...]
In Lua, I write tree = {a, b, c, d} where a,b,c and d are previously defined trees. If a tree has no children, an empty list: tree = {}. If I want to avoid using temporary variables, I can write it all at the same time. alice = {{{{},{}},{}}}. Alice's first (and only) child is alice[1], which happens to be Orange. Pink is {{},{}}, etc. Now the first thing we have to do is find a way to compare tables.
Indeed, when I write blah = {}, a new table is created in memory. When I write alice = {{{{},{}},{}}}, 6 new tables are created in memory. And most importantly, if I write
foo = {}
bar = {}
I will have created two different tables, and foo will not be equal to bar. How do I tell if two trees are equal?
There is an easy way to know if they are different. Their sizes. If A has 3 nodes, and B has 7, clearly, A and B cannot be equal. Let's first see how to get the size of a tree. The recursive definition makes it quite easy. The size of A is the sum of sizes of its children + 1 (its own node). In pseudo-code:
function size(tree) sum = 0 for all child in tree do sum = sum + size(child) end return sum + 1 end
This is a recursive call to size(): before giving the size of a tree, the size() function has to compute the sizes of the subtrees first, and calls itself on them. If we follow the calls to size(), we get this kind of path:
This kind of traversal of the tree (a sequence that goes to every node in a certain order) is called "depth-first". Indeed, we always go as deep as possible before going back up. Numbering the nodes according to the order of depth-first traversal gives:
This order of traversal is very important. We will use it a lot. For instance right now. We wanted to define a relation between the trees using their sizes. If size(A) < size(B), then A < B. If size(A) > size(B), then A > B. The tricky part is of course if A and B have the same size. Obviously there are many trees of the same size, that are not equal. The idea is to think recursively. If A and B have the same sizes, compare their first children instead. If these are equal too, compare the second children, etc. If all the children are equal, then given the recursive definition of trees, the trees are equal. Let's make a compare function, that return -1 if the first argument is smaller, 1 if is bigger, and 0 if they are equal
function compare(A,B) if size(A) < size(b) then return -1 elseif size(A) > size(b) then return 1 end for all pairs a,b of children of A and B do if compare(a,b) is not 0 then return compare(a,b) end end (after the loop, we know that all pairs of children are equal, therefore A and B are equal) return 0 end
Now of course, this is pseudo code, you have to take care of the case when A and B have a different number of children: if the loop went through all A's children and that B has more, B is bigger (an empty tree is smaller than any other tree). But that's detail. The point is, we now have a total order over rooted trees: any two trees are always either equal, or one of them is bigger. This allows to sort the trees in order, like we would sort numbers. And this is pretty nice, since now, we can take any two separate trees with our abstract representation in memory, and decide if they are equal.
I lied a bit. I said we were representing rooted trees in memory. It's almost correct. Take a look at these two, and see if you can find the problem:
The one of the left is Bob's second cousin, Alfred. And the one on the right is... Wait. Alfred too. He's just not drawn the same. But if you represent them in memory as they are drawn here, you get:
alfred1 = {{{},{}},{},{}}
alfred2 = {{},{},{{},{}}}
If you compare them using our compare() function, what happens? Both trees are size 6, so we have to try the children. First pair of children: alfred1[1] is size 3, and alfred2[1] is size 1. The function returns and tells us that alfred1 > alfred2... Ouch, where's the bug?
No bug here. Our compare() function doesn't compare rooted trees. It compares ordered rooted trees. Another kind of trees. "Oh no, one more tribe!" Sadly (for us) yes. Because, remember, we defined a rooted tree as "a set of rooted trees". However, for the computer, a rooted tree is a list of rooted trees. A list keeps its element in a certain order (usually the order they've been put in). There's the first, then the second, and the third, and so on. The mathematical set, on the other hand, doesn't have any order. An object is in it, or not. For a set of M trees, there are M! possible lists of them (again, minus the possible repetitions if some trees are equal). "Oh no, we're doomed!" No so much. Thanks to our ordering function itself.
Since our order relation on trees is total, we can sort trees. And there is a unique way to write a list of trees in increasing order. Think of numbers, given a bunch of numbers, you can always put them in order, and there is only one way to do it. Same for trees. So even if for a tree with M children, there are M! ways to represent it in memory, there is only one of these ways that has the children in increasing order. We pick that one, and say that it is the unique representation of our (unordered) rooted tree.
Actually, I chose to pick the decreasing order. It has the same properties (it is unique), so it shouldn't be a problem. Why? Because later on, it will make some trees more beautiful. And math, believe it or not, is all about beauty.
Programmatically, what does it mean? Just sort the tree's children in decreasing order before doing anything else. That will ensure we have this unique form for the unordered rooted tree, instead of having one of the M! others. I call this process "canonizing" the (memory representation of the) tree. (Note that for a tree to be canonic, its children should be too. Quite naturally, the canonizing function is first applied recursively on the children, before sorting them in decreasing order).
Where are we? We have data in memory, which truly represents rooted trees uniquely. We are able to compare and sort them, test for equality. What about creating some trees? The initial goal was to make all trees of size N. How do we do that?
My first approach was exactly the one I had used on the paper. Take a tree of size N. Write it down N times. Add a new node to each of these new trees, each time as a children of a different node.
Tadaa! Now of course we need to canonize them, and remove the duplicates. Remains:
Think about this: if you take any tree of size N, and remove a node from it, you get a tree of size N-1. So all trees of size N are actually trees of size N-1 with an additional node. By generating all "plus one" trees from the N-1 list, and cleaning the duplicates, we should get all rooted trees of size N.
Programmatically, how do we do make the "plus ones" from a given tree? By traversing it, and at each node, adding a child, saving this N+1 tree somewhere, and removing the new child before going on (or else, the new tree would get N new nodes: one per original node...) Then we can canonize all these new trees, sort them, and remove the duplicates. If we do this for every rooted tree of size N, we should end up with absolutely all rooted trees of size N+1. Now we just need to start somewhere. The list of all rooted trees of size 1 is pretty short, there is only {}. Apply the generating function once, you get {{}}. Once more, {{{}}} and {{},{}}. Once more, {{{{}}}}, {{{},{}}}, {{{}},{}} and {{},{},{}}. And so on.
Up to N = 5:
{}
{{}}
{{},{}}
{{{}}}
{{},{},{}}
{{{}},{}}
{{{},{}}}
{{{{}}}}
{{},{},{},{}}
{{{}},{},{}}
{{{}},{{}}}
{{{},{}},{}}
{{{{}}},{}}
{{{},{},{}}}
{{{{}},{}}}
{{{{},{}}}}
{{{{{}}}}}
The number of unique rooted trees we get for the first ten N is:
1: 1 2: 1 3: 2 4: 4 5: 9 6: 20 7: 48 8: 115 9: 286 10: 719
Guess what? It works. These are the same numbers you can find on MathWorld or the On-Line Encyclopedia of Integer sequences. Pretty cool huh? Well, I found it pretty cool, at least. I was only one step away from the free trees.
But of course I took the long way home.
There is a little problem with recursive functions: they can be very slow. Indeed, they have to call themselves on other objects (here, the subtrees), and there call themselves again on other objects, an so on, until a object simple enough is found, whose result does not depend on other objects (here, the leaves: no children, size is 1). Every time we call the size() function on a tree, the whole tree is traversed, every node is visited, and only then everything is summed up to give the final result. Keep in mind that the size of a tree is required by many other functions: canonizing, comparing, sorting... Sorting, for instance, has to compare pairs of trees many times. And every time, the size() function is called. That's a lot a tree traversals...
It is fine for small trees, and for a small number of trees. But when we get to, say, 20 nodes, there are 12,826,228 trees. At 30 nodes, 354,426,847,597. Combinatorial explosion, they call it. Clearly we won't get that far, but even for smaller numbers, we have to keep in mind that computers are not infinitely fast. Generating the 20299 trees up to size 13 took about 4 minutes on my moderately powerful computer. Not too bad, but we can probably to better.
A good way to speed up recursive functions is to save the intermediary results, whenever possible. If instead of calling the function on a certain object, we can simply read the value somewhere, surely this will be faster. If the result has not yet been computed, then do it the normal way, and save the result for future use.
For the tree size, I store it directly in the root node (Lua tables can work both as lists and records/tables, at the same time. Quite handy!) The first time we call size(tree), tree doesn't yet know its size, so the function is called recursively on children, which themselves ignore their own size for the moment. The whole tree is traversed, and before each size call returns, it saves the answer in each node. Result of the operation: every subtree knows its size. Example on Alice:
To be sure to speed up things, we can systematically compute the sizes before anything else. Do it once, use it everywhere. Now if you take for instance the comparison function. We know if first compares sizes of the trees. No need to go through all the nodes, the information is right there! We have to dig deeper only if the sizes are equal. And even then, comparing the first children can be reduced to comparing two numbers, which have been precomputed also. Surely this is faster.
Then I got an idea. Comparing trees now reduces to comparing numbers stored in these trees. Maybe we could keep the numbers and get rid of the trees altogether... Since we designed the comparison function to traverse the tree depth-first, we know that the sizes are going to be compared pair by pair, in the depth-first traversal order, until we find a difference or until we've seen that all the pairs are equal.
Let's do that then. Represent a tree by the sequence of its nodes sizes, written in depth-first traversal order. Since comparing these sequences is in fact - behind the scene - what does the comparison function with trees, we know that it will lead to the same result. Two identical sequences represent the same tree, and two different ones have to represent different trees.
I, displaying a tremendous lack of imagination, called these sequences "names". For instance, the name of Alice is 6-5-3-1-1-1. Alfred's is 6-3-1-1-1-1.
Two notes at that point:
Wait, wait, we have this new shiny name thing, and we still need to go through a tree to canonize it? What's the point then?
Names are a lot easier to handle. Comparing them is not recursive anymore, but iterative ("loop until you find two different numbers"). They use less memory: they are N numbers in a list, instead of N lists of references to other lists (in which anyway we put the very same numbers). They are a lot easier to read too.
The names keep the recursive nature of the rooted trees. If you analyze a bit, you can see that the name of a tree is its size, followed by the names of its children.
It is quite easy to separate a subtree from the tree: if an element of the name says x, the tree it represents is itself and the x-1 following nodes. Similarly, we can build a tree out of a name. Take out the first element of the list (the size) and divide the rest into the names of the children (here, (3,1,1), (1) and (1). Call recursively the function with the children's names as arguments, and add the returned trees as children. Piece of cake.
After looking at tree names for a little while, you get used to them, and they become a lot easier to read than the tree representation. Compare {{{{{{},{},{},{}}}},{{{}}}}} and (12,11,7,6,5,1,1,1,1,3,2,1). We can see patterns emerge. A chain is a list of consecutive numbers. A root N followed by N-1 ones makes a kind of rake or hand.
And most of all, you can tell the size of the tree by just looking at the first number, while counting opening brackets is a bit annoying. To be honest, I really like the tree form too. It makes mesmerizing animation patterns when it scrolls in a terminal (yes, I did spend some time watching the output of the programs unroll as the trees were computed. Hey, some people have fishtanks...)
So, super cool, we have another way to represent rooted trees. Maybe we can generate them directly as names?
That's another job for Captain Recursivity!
Recursivity makes things quite easy. To make a tree name of size N, we need to write down "N" followed by names whose sizes add up to N-1. A list of tree can be called a forest. So, to make all trees of size N, generate all forests of size N-1, and write N at the beginning of each of them. We haven't solved anything yet, just moved the problem: how do I generate a forest of size N-1? Or N, for that matter...
Just notice that a forest of size N is a tree of size x followed by a forest of size N-x. Oh, hello, recursivity! To make all forests of size N, pick all possible pairs of "tree of size x" and "forest of size N-x", for x going from 1 to N. That should do the trick. Now of course it implies that you already have computed trees and forests of size inferior to N. Here too, we could either simply write a recursive call to the generating function, or cheat and save the generated trees somewhere. Obviously the second one is faster and therefore is our choice.
Don't forget to clean up a bit: canonize all these names, sort them, remove duplicates, and ooh, magic, we get the same trees than with the other method. Wonderful.
Again up to N = 5:
1 2 1 3 1 1 3 2 1 4 1 1 1 4 2 1 1 4 3 1 1 4 3 2 1 5 1 1 1 1 5 2 1 1 1 5 2 1 2 1 5 3 1 1 1 5 3 2 1 1 5 4 1 1 1 5 4 2 1 1 5 4 3 1 1 5 4 3 2 1
We now have two ways of generating all rooted trees of size N. We want all free trees of size N. Pretty close. We have seen before that to each free tree of size N corresponds a certain number of rooted trees (at most N, usually less due to symmetries). Likewise, to each rooted tree corresponds one free tree, obtained by forgetting about the root. Going a bit further we can say that to each rooted tree corresponds a certain number of other rooted trees, who share the property of having the same free cousin. In mathematical terms, we can call this an equivalence class. To go from the list of rooted trees to the list of free trees, we need to group them into equivalence classes.
Each class (composed of a certain number of rooted trees) will represent a unique free tree. Then we can pick, for instance, the biggest rooted tree in the class to represent the free tree uniquely.
To classify a rooted tree, we have to generate all its class members, and pick the biggest. In other words, pick all possible roots in the equivalent free tree. This is where I use, finally, the graph representation of trees. Indeed, the recursive tree representation has a major drawback: you cannot move from a subtree to its parent. It simply does not have the information. However, since we are going to need to change the root, the parent -> child relationships are going to change. One solution would be to give to each node a reference to its parent. But, remember the comment I made about having an ancestor as child? Doing this effectively turns the tree into a kind of bastardized graph, both tree and directed graph at the same time. Let's use a true graph representation, and things should go smoothly.
Turning a rooted tree into a graph is easy. First label the nodes by depth-first traversal (or any other order, actually). Then traverse the tree, and at each node N, add each child C as an edge (N,C) in the graph.
Turning a graph into a rooted tree is a bit trickier, but not that much. First pick a node as the root. There are N ways to do that, which is evidently related to the fact that a free tree has at most N rooted cousins. From this root, we are going to do a depth-first traversal of the graph.
What? For now we've always spoken of depth-first traversal of a tree, not a graph. Well, it's possible too, and it's one more proof that trees and graphs are related species. You can do depth-first traversals of graphs with cycles, they just have to be connected and simple.
The only trick is to mark the visited nodes, to be sure that you don't visit them again. When calling the function on a node of the graph: mark it visited, get all its unvisited neighbors, call the function recursively on them, and add all returned trees as children. It looks almost too easy. It's pure magic.
From one rooted tree, make a graph. From this graph, make all N possible rooted trees. Canonize, sort, trim, you get its equivalence class. Pick the biggest in it, you have the unique representation of the equivalent free tree.
From the list of generated rooted trees up to size N, replace each tree by its equivalent free tree. Sort, trim, you end up with the list of free trees up to size N.
Done.
Or even better, do that at each iteration of the generation algorithm. Do the "add one node" thing on the list of free trees of size N-1 instead of the list of rooted trees of size N-1. The sooner we reduce the list, the better: we generate less duplicates, it takes less time to process.
Results are the same, of course. Look, here are our friends from the first image. Can you recognize them?
{}
{{}}
{{{}}}
{{{},{}}}
{{{{}}}}
{{{},{},{}}}
{{{{},{}}}}
{{{{{}}}}}
{{{},{},{},{}}}
{{{{},{}},{}}}
{{{{},{},{}}}}
{{{{{}},{}}}}
{{{{{},{}}}}}
{{{{{{}}}}}}
The list goes on like this:
1: 1 2: 1 3: 1 4: 2 5: 3 6: 6 7: 11 8: 23 9: 47 10: 106 11: 235 12: 551 13: 1301 14: 3159 15: 7741
Again you can check on MathWorld or the On-Line Encyclopedia of Integer sequences that they match. They do.
It is done. Now remember when I chose to sort subtrees in decreasing order when canonizing? I said it made some trees more beautiful later. Later is now. In fact it is not really true anymore, but it made sense at some point during the coding. Indeed, initially I chose to pick the smallest rooted tree in a class as the representation of the free tree.
Consider the chain of size, say 5. If you pick the root to be one extremity, its name is 5-4-3-2-1. If you pick the second node and canonize in increasing order, you get 5-1-3-2-1. The third node: 5-2-1-2-1. Picking nodes 4 and 5 give equivalent trees (a chain is symmetrical).
When you classify it by picking the smallest tree, it yields 5-1-3-2-1. Quite frankly, it's ugly. A chain should look like a chain. I wanted the algorithm to give me the nice and obvious 5-4-3-2-1. So I changed the canonizing order to decreasing. It gave, for the 5-chain:
5-4-3-2-1 5-3-2-1-1 5-2-1-2-1
The smallest one is now 5-2-1-2-1. At least it is symmetrical, so it is a bit better. But still not good enough. So I switched to picking the biggest one in the class.
In fact, changing the canonizing order was not necessary, simply taking the biggest one, even with increasing canonizing order would have been enough, to achieve my requirement on the chain. But I found afterwards that sorting subtrees in decreasing order makes all other trees nicer. They have a more regular look when the big trees come first. The names are easier to read. It's probably just a matter of taste.
So yes, I rewrote parts of the code, and regenerated the thousands of trees only so that chains looked better. Very futile, but futility and beauty make our existences more meaningful.
And as I said, math is all about beauty.
Here I took a bit of rest, a good night's sleep (well, it was day already, but...) and went on to the second part of my task. Drawing all these trees.
You see, even if I got to love these many brackets and sequences of numbers, they are not very visual, to say the least. My initial goal was indeed to make the machine draw all these trees for me. Well, it was a lot easier than I feared.
The problem is to place dots linked by lines on a two dimensional plane, in a pleasing way. By pleasing I mean:
Algorithmic placement of each node one by one seemed pretty daunting. All these conditions (and I suppose, my educational background) suggested instead a physical approach.
Give each node a certain mass. Link neighbors by springs with a certain rate and equilibrium length. Link non-neighbors by repulsive forces. Apply some damping to reduce the energy of the system and make sure that the oscillations fade away. Integrate speed and position using the good old Euler method, well known by all video game developers.
Launch simulation, wait for convergence. Tadaa.
Now of course, there are lots of details to take care of. Initial position of the nodes can be random. Choosing parameters such that convergence is quick but still retains the "nice" properties we wanted requires a bit of tweaking. You can also put a limit on the number of iterations for some rogue cases that for some reason refuse to converge. You also have to worry about centering all these dots, computing a bounding box, translating everyone inside the image, etc. But in the end, it worked like a charm.
For the actual "drawing" of the image, I chose to output the graphs in SVG. Since it is a text based format (XML), it is quite easy to generate programmatically. Do not worry about pixels: let other applications do the rasterization.
Here is, for instance, our buddy 3-2-1:
]]>
And since a picture is worth a thousand words, four or five pictures should save me quite a lot of typing.
Here ends our beautiful adventure of digital gardening, of planting binary seeds and watching them unfold their mathematical beauty. The magic occurred, and I hope I could, for a little while, share a bit of this magic. Amaze you as they amazed me. Put a lot of stars in your eyes.